Cauchy Schwarz Inequality for Integrals
View course details in MyPlan. Markov and Chebyshevs inequality.
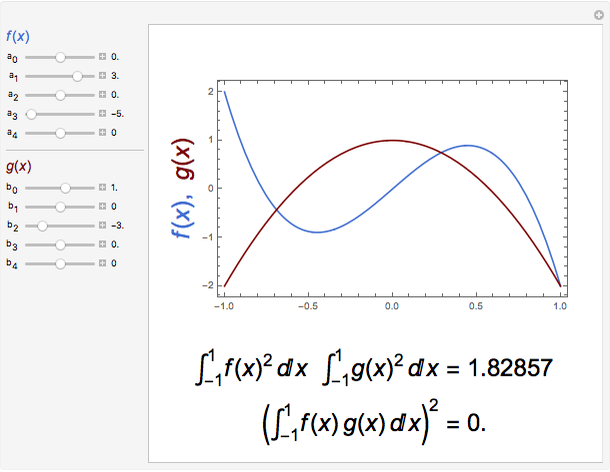
Cauchy Schwarz Inequality For Integrals Wolfram Demonstrations Project
Either a minimum grade of 20 in MATH 126 or a minimum grade of 20 in MATH 136.

. The symmetry is the assertion that the second-order partial derivatives satisfy the identity. Transformations of a single random variable. Substancial - Free ebook download as Text File txt PDF File pdf or read book online for free.
Many real-life systems are described by differential equations. To analyze such systems when randomness is involved we often need to differentiate or integrate the random processes that are present in the system. Derivatives and Integrals of Random Processes.
In mathematical analysis the Minkowski inequality establishes that the L p spaces are normed vector spacesLet S be a measure space let 1 p and let f and g be elements of L p SThen f g is in L p S and we have the triangle inequality with equality for 1 p if and only if f and g are positively linearly dependent ie f λg for some λ. Jointly with STAT 394. In mathematics the symmetry of second derivatives also called the equality of mixed partials refers to the possibility of interchanging the order of taking partial derivatives of a function of n variables without changing the result under certain conditions see below.
Contains some random words for machine learning natural language processing. Weak law of large numbers for finite variance.

Real Analysis Question About Proof Of Showing Cauchy Schwarz Inequality Implies Schwarz Inequality From Spivak Mathematics Stack Exchange

Proof Of Cauchy Schwartz Inequality Mathematics Stack Exchange

Solved The Inequality Below Is Called Cauchy Schwarz Chegg Com

Solved 2 The Cauchy Schwarz Inequality For Integrals Chegg Com
0 Response to "Cauchy Schwarz Inequality for Integrals"
Post a Comment